BibTeX

Overview of our approach, FoVer. We train PRMs on step-level error labels automatically annotated by formal verification tools on LLM responses to tasks compatible with formal verification. We observe that the resulting LLM-based PRMs improve verification across broad reasoning tasks.
Process Reward Models (PRMs), which provide step-by-step feedback on the reasoning generated by Large Language Models (LLMs), are receiving increasing attention. However, two key research gaps remain: collecting accurate step-level error labels for training typically requires costly human annotation, and existing PRMs are limited to math reasoning problems.
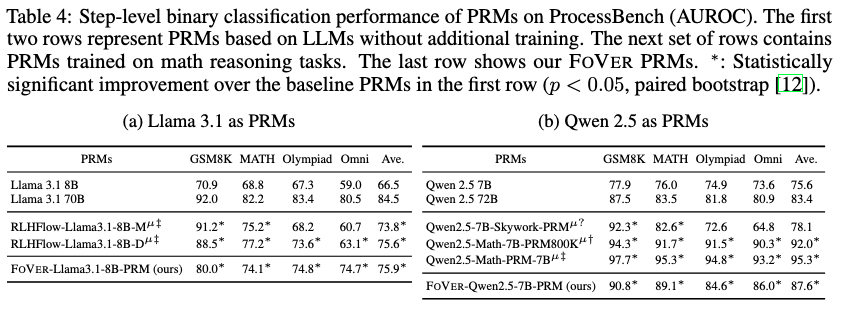
In response to these gaps, this paper aims to address the challenges of automatic dataset creation and the generalization of PRMs to diverse reasoning tasks. To achieve this goal, we propose FoVer, an approach for training PRMs on step-level error labels automatically annotated by formal verification tools, such as Z3 for formal logic and Isabelle for theorem proof, which provide automatic and accurate verification for symbolic tasks.
Our experiments highlight the following findings:
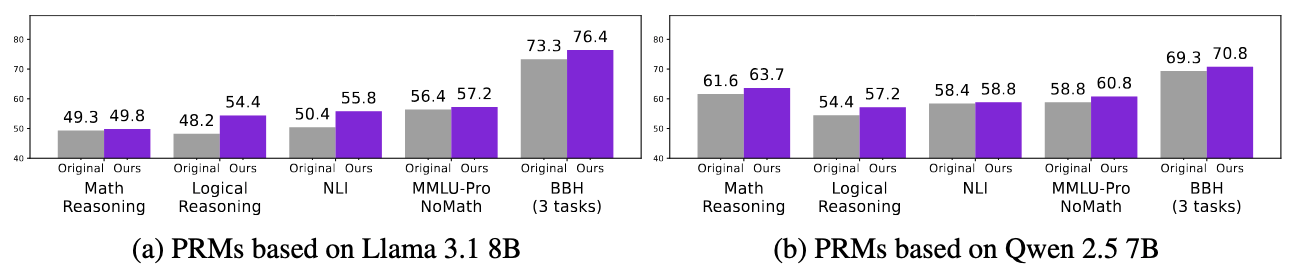
Best-of-K (K=5) performance of PRMs on 12 reasoning tasks. FoVer creates training datasets for PRMs on tasks where we can automatically annotate step-level error labels using formal verification tools. FoVer significantly improves verification performance on broad out-of-distribution reasoning tasks, compared to baseline PRMs based on the original LLMs.
 Dataset
Dataset
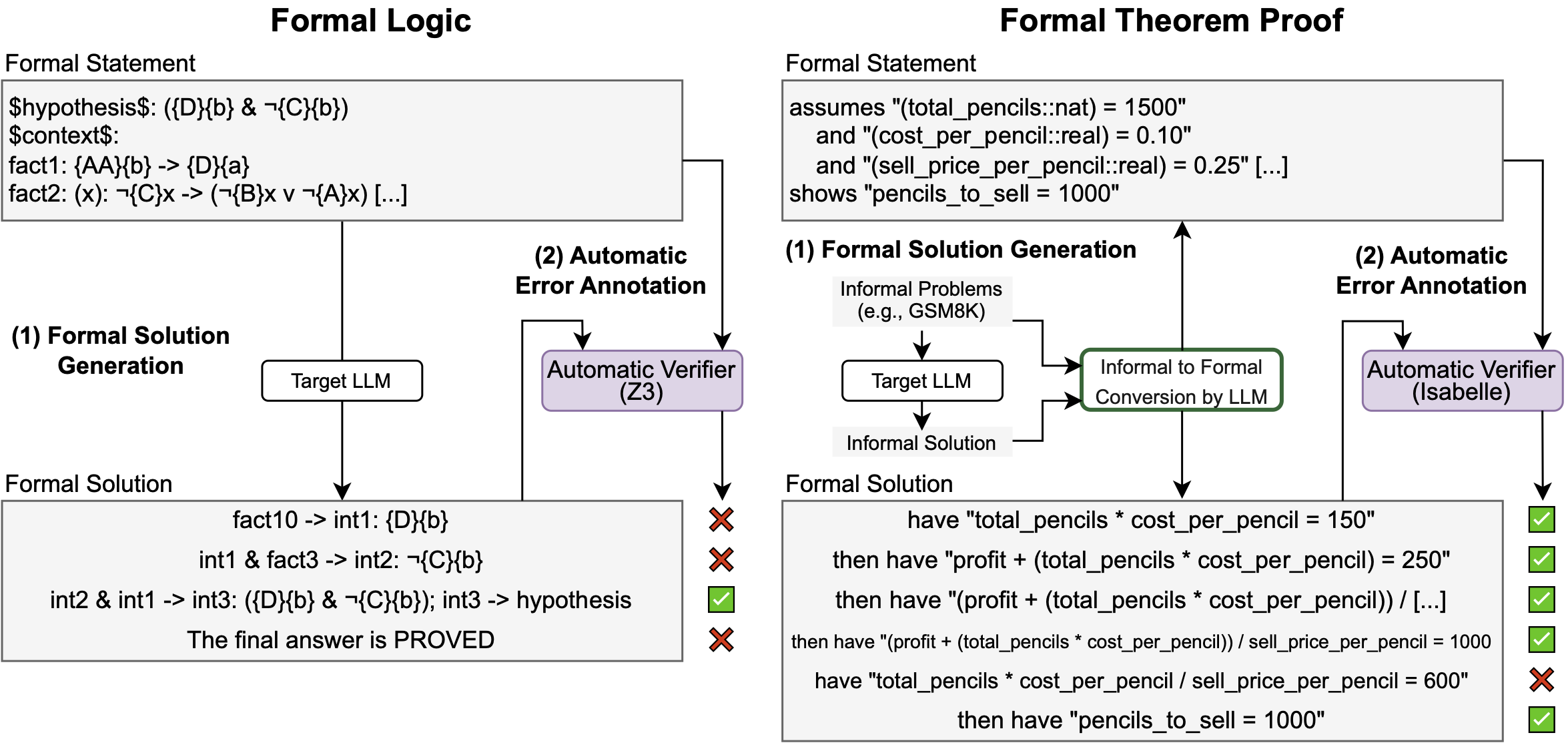
Creation process of the FoVer dataset.
(1) We first generate LLM reasoning in the format compatible with formal verification tools: Z3 and Isabelle.
(2) We use the formal verification tools to automatically annotate step-level error labels, without involving human annotation.


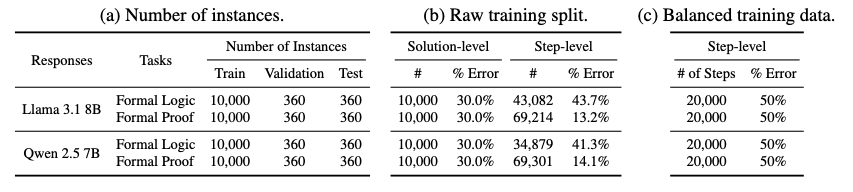
Statistics of the FoVer dataset.